4月15日に北海道大学の西浦博教授が、このまま人と人との接触を減らす対策を何も取らないと最悪で42万人が死亡する恐れがあることを発表しました。西浦教授が何の裏付けもなく、単なる「勘」だけでこの数字を挙げることは考えにくいと思われますが、この数値を否定する人も多くいます。 　その中には、西浦教授の発言の仮定である「対策を何もとらないと」を見落として、これがデマであると発言したり、直感だけで「そんなことあるはずがない」と否定する人が少なくなかったことは残念です。もちろん、西浦教授がこれまで試算の方法を詳しくは語らない傾向がありますので、他の専門家が検証のしようのないこともそのように言われる原因です。 　さて、これまで西浦教授は、感染症の蔓延モデルであるSIRモデルを用いているのではないかと言われていますので、このモデルからわかることをここで述べ、決して煽るわけではなく、数式から機械的に得られる結果を共有しましょう。各都道府県の知事が、以下の結果を見てくれていたらと願っています。以下の結果は、同じ数値を使う限り、誰が何回計算しても同じものが得られます。 　SIRモデルとは、次の3つのグループに属する人数の関係を記述したものです。 ●グループS:感染する可能性のある人(Susceptible) ●グループI:感染者(Infected) ●グループR:感染から回復した人(Recovered)あるいは感染させる心配がなくなった人 　ここで、注意してほしいのは、感染者であってもPCR検査によって発見され隔離されている人は、他の人に感染させる心配はないので、グループRに入ります。グループIに入る人は、まだ発見されずに「野放しになっている感染者」を指し、ここでは誤解を避けるため、以後は「市中感染者」と表現することにします。 　SとIとRの人数は時間によって変化しますので、それぞれ時刻tの関数となります。SIRモデルはS、I、Rの人数の時間に対する変化を表した数式なのですが、高校数学程度の知識で、SとIの関係を導くことができます。(数学が得意な高校生向けの題材になります。) 　そこから感染が終わった段階での死者数を求めるには、致死率と対象地域の人数と初期の情報が必要になります。初期の情報とは、観測開始の段階でS、Iの人数、観測開始の段階で1人の人が感染させる人数(これを基本再生産数といいR0で表します)のことです。 　ここでは、仮に致死率を3％、最初の段階での市中感染者の割合を0.01％と定めます。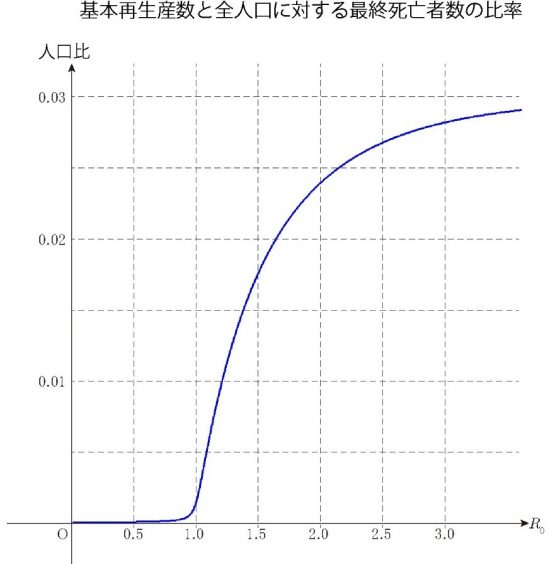 　このもとで、何も対策をとらなかった場合のR0と最終死者数比Dの関係は次のグラフのようになります。 　なお、致死率が1.5％になったとすれば、この表のDの値は半分になります。さて、このグラフでは、R0=2.5の場合、人口の2.7％、すなわち、320万人くらいが最終的に死亡することになりますが、これは西浦教授の試算(42万人)よりかなり多くなります。したがって、これとは違う設定を考えていたことになりますが、その設定の修正の一つについては後述します。 　それよりも大切なことは、このグラフの形です。R0が1を超えるとDの値は急激に上昇します。ゆっくりと増えるのではありません。このようにR0が1を超えたあたりでは、少しの違いで大きく結果が異なりますので、今後は、その日ごとの一人の感染者が感染させる人数「実行再生産数」(RあるいはR(t)で表します)をできる限り早く対策を取り小さくすることが肝要なのです。 　1人の市中感染者が多くの人に感染させないため、すなわち、実行再生産数を減らすために「すぐに」できることは大きく2つあって、一つは人と人の接触を減らすこと、もう一つは、できるだけ早く市中感染者を多く発見して隔離することなのです。