新型コロナウィルスの感染拡大が止まらないことで、様々な休業、外出の自粛要請が出ています。その要請の根拠は厚生労働省のクラスター対策班による「図」によるところもあります。これはクラスター対策班の北海道大学の西浦博教授が提示したものをもとに作成されたものです。 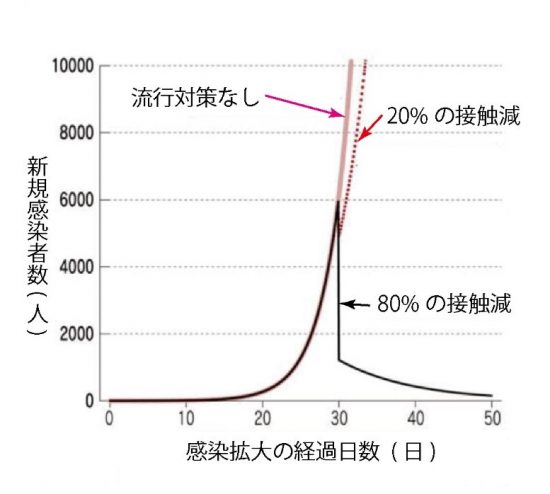　この図は、感染が始まってから30日後に感染抑制措置をしない場合とする場合で、新規感染者数がどのように変化するかを表したグラフです。多くのメディアで使われているものの、テレビなどの報道で一部誤った認識、解説が流れていることもあるので注意が必要です。その誤った報道の部分も含めて、極力、数学が苦手という人にもこのモデル全体を理解してもらえるように説明していきます。 　なお、これはあくまでも「数理モデル」ですので、状況をかなり単純化しています(それ自体は悪いことではありません)。したがって、現実はこの図のようになるとは限りませんが、似たような動きはすることは考えられますので、ある程度は有用です。また、これ以外のモデルもありますが、西浦教授は、この分野の第1人者ですので、もちろんそれを知り得たうえでこのモデルを採用したと考えられます。 　まず、人間を次の3タイプに分けます。 (S)感受性保持者(Susceptible): まだ感染していないが、感染する可能性がある人(今のところの多くの人がこれにあてはまる) (I)感染者(Infected): ウィルスに感染中で、他人に伝染させる可能性のある人 (R)免疫保持者(Recovered): 感染状態から回復するかワクチンなどを打つことで免疫をもち、ウィルスを自己体内で消滅でき、他人に感染させる恐れのない人。「隔離者(Removed)」などとも呼ばれ、死者も隔離者の一部とみなします。 　これは、このように人間を(S)、(I)、(R)の3つに分け、その移動を考えたものなので、SIRモデルといいます。 　ある日(これを感染が広がり始めてt日目とします)における(S)、(I)、(R)の人数をS(t)、I(t)、K(t)とおきます。すなわち、次のようになります。 S(t)は、t日目の感染していない人の人数 I(t)は、t日目の感染者の人数 K(t)は、t日目の段階で感染から回復した免疫保持者、他人に感染させることのない人の人数 　ここで、(R)の人数をR(t)としないのは、後で出てくる文字との重複を避けるためです。 　さて、(S)、(I)、(R)の人数は次の法則で移動するとします。(実際は異なりますが、単純モデルとしてこう考えるということです) 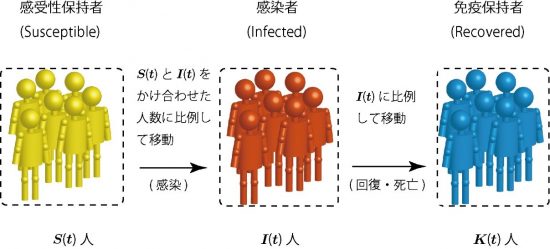感受性保持者　S(t)人 ↓S(t)とI(t)をかけ合わせた人数に比例して移動 感染者　I(t)人 ↓I(t)に比例して移動 免疫保持者　K(t)人 　数学がわかる人のためにこのことを式で表すと次のようになります。βとγは正の定数です。tは連続変数として扱います。なお、この式がわからなくても後の話には困りません。 dS(t)/dt=-βS(t)I(t) dI(t)/dt=βS(t)I(t)－γI(t) dK(t)/dt=γI(t) 　西浦教授の図では、縦軸は新規感染者数なので、ここではS(t)(感染する可能性のある人の人数)の減り方が問題になります。これは、数学の表記は-(dS(t)/dt)となりますが、これをN(t)で表すことにします。すなわち、西浦教授の縦軸がN(t)です。 　以上の数式から、複雑な作業といくつかの近似を行ない、このN(t)(新規感染者数)は次のように表せる(近似できる)ことが知られています。 N(t)=(定数)e^at 　突然現れたeとかaとかは何なんだと思われる方もいらっしゃるでしょう。まず、eについてですが、これは数学でよく用いられる定数でおよそ2.7です。したがって、この式は、 (新たな感染者数)=(定数)×(2.7)^(a×(日数)) と表すことができます。なお、新規感染者数の爆発的に増えるか終息するかの議論をするときは(定数)の値は重要ではありません。 　次に、aについてですが、この値は本当はS(t)(まだ感染していない人の人数)によって変わるので定数ではないのですが、そもそもこのモデル自体が感染流行初期を想定しているため、最初の数値と大きく変化していないと考えて定数の扱いをしています。aは観測値(20日目で300人、30日目で6000人)からおよそa=0.29であることがわかります。 　一方、理論的な計算からa=γ(R_0-1)が導かれます。ここで、R_0は基本再生産数といい、初期の段階で一人の人が感染させる人数を表します。(本当はR_0の部分にR(t)(実行再生産数という)をあてるべきですが近似しています。) 　このR_0の値を西浦教授は、ドイツ並みのR_0=2.5と考えているようです。これによって、γ=0.193⋯≒0.2(もちろん近似値です)がわかります。話が難しくなってきましたが、要するに、 a=0.2×(1人が感染させる人数-1) ということです。大切なことは、新たな感染者数が増えるか減るかは、このaの値が0より大きいか小さいかによって大きく異なってくることです。何も措置をしなければa=0.29ですので、感染拡大から30日以降、爆発的に増えます。これに対し、西浦教授の案は、人と人の接触を断つことで、このaの値を下げ、0より小さくするのがねらいです。なお、 20％減ならa=0.192 40％減ならa=0.094 60％減ならa=-0.004 80％減ならa=-0.101 となり、60％減からはかろうじてaは0より小さくなるものの新規感染者数はほぼ横ばいのままで、もしも来年東京オリンピックを開催するのであれば、その準備期間も考えれば間に合いません。60％減の場合の半減期(半分に減るまでの期間)はおよそ半年後です。仮に、今が、最初の図の「30日目」であるとすると、半年後にも1日1200人の新規の感染者が出て、今から1年後にも1日600人、オリンピック中も少なくとも1日300人の新規感染者が出ることになります。 　なお、このモデルに従えば、70％減の場合の半減期はおよそ13日、80％減の場合の半減期はおよそ7日になります。ですから、「強い措置を短期間行なう」ことが大切で、様子を見ながらの緩い措置では、非常に長い期間がかかります。