最近の報道番組等を見ていると一部ですが、最初のグラフが「感染者数」(先ほどのI(t)の値)と誤解して説明していらっしゃる方を見かけます。また、政治家の方にもいらっしゃいます。そのような方は、「なぜ、80%の接触減で感染者数がこんなに減るんだ」と発言されますが、「感染者数」はそんなに急には減りません。先ほどのグラフは「感染者数」ではなく、「
『新規』感染者数」なのです。ですので、抑制措置をした30日目に(このモデルの理論上は)ガクンと減るのです。
一つ簡単な例で説明しましょう。29日目に感染者が1000人いたとして、何も流行対策をせずに30日目に感染者数が1100人になったとしましょう。この場合は先ほどのグラフには新たな感染者数として「100人」と記載されます。
しかし、80%の人が外出を控えれば、1000人の感染者のうち200人が外出し、この200人が感染者を20人増やしますので、グラフには増えた分の「20人」(先ほどの100人の5分の1)が記載されます。そこから、それぞれのaの値ごとに曲線を伸ばしていけばよいのです。
次の図を参考にしてください。30日目の新規感染者数は、例えば、80%減なら流行対策なしの80%減の数値から開始されています。
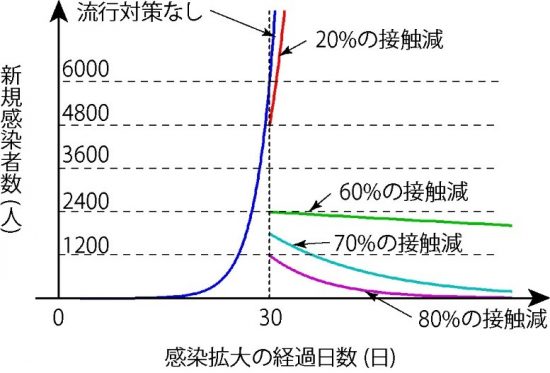
最初の図と違うように見えるのは、最初の図は29日目と30日目をおそらく直線で結んでいるからです。これは、感染爆発をするかどうかの議論には影響ありません。
以上で、クラスター対策班が使用しているSIRモデルについて説明してきました。このモデルはたくさんあるモデルの1つにすぎないことをこれまでも述べてきましたが、最後にこのモデルに従った結論を記しておきます。今、最初のグラフの30日目の状態になったとして、次のことがいえます。
(1)外出制限が50%以下ならば、感染爆発、医療崩壊が起こる。
(2)外出制限が60%ならば、2年経っても一日の新規感染者数は100人を切らない。
(3)外出制限が70%ならば2か月程度で一日の新規感染者数は100人を切る。
(4)外出制限が80%ならば1か月程度で一日の新規感染者数は70人程度になる。
西浦教授が、外出要請の80%減を提示したときに、「60%にならないか」「70%では無理か」などの「値引き交渉」が始まったと発言されています。
「値引き」をするとどうなるかを政策決定者は深く理解する必要があります。
相手はウィルスなので、「法の解釈を変える」「閣議決定でなかったことにする」あるいは「科学者を恫喝する」ことによって変わるものではないのです。
なお、この記事のテーマとはずれますが、外出制限と営業自粛だけではなく、PCR検査の問題点は多いもののそれでも検査体制を整えることなど、いくつかの別の方法もあることも記しておきます。
<文/清史弘>
せいふみひろ●Twitter ID:
@f_sei。数学教育研究所代表取締役・認定NPO法人数理の翼顧問・予備校講師・作曲家。小学校、中学校、高校、大学、塾、予備校で教壇に立った経験をもつ数学教育の研究者。著書は30冊以上に及ぶ受験参考書と数学小説「数学の幸せ物語(前編・後編)」(現代数学社) 、数学雑誌「数学の翼」(数学教育研究所) 等。
 最初の図と違うように見えるのは、最初の図は29日目と30日目をおそらく直線で結んでいるからです。これは、感染爆発をするかどうかの議論には影響ありません。
最初の図と違うように見えるのは、最初の図は29日目と30日目をおそらく直線で結んでいるからです。これは、感染爆発をするかどうかの議論には影響ありません。
 最初の図と違うように見えるのは、最初の図は29日目と30日目をおそらく直線で結んでいるからです。これは、感染爆発をするかどうかの議論には影響ありません。
最初の図と違うように見えるのは、最初の図は29日目と30日目をおそらく直線で結んでいるからです。これは、感染爆発をするかどうかの議論には影響ありません。