数学教育の専門家が見た、大学共通テスト「記述式以外」の問題点<短期連載:狙われた大学入試―大学入学共通テストの問題点―>
文科省が入試改革で「失った」ものとは?
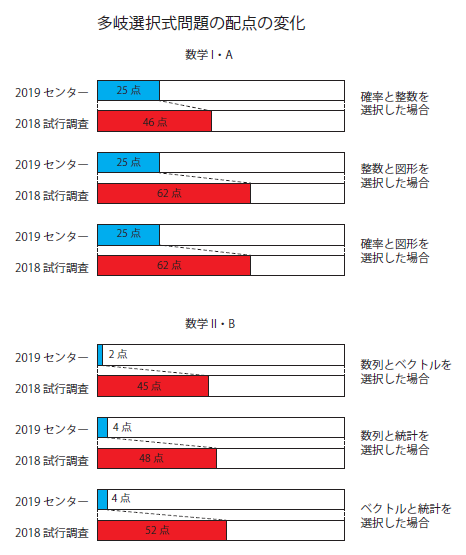 【多岐選択式問題の配点の変化】
▼数学I・数学A
(1)確率と整数を選択した場合
2019センター:25点 2018試行調査:46点
(2)整数と図形を選択した場合
2019センター:25点 2018試行調査:62点
(3)確率と図形を選択した場合
2019センター:25点 2018試行調査:62点
▼「数学II・数学B」
(1)数列とベクトルを選択した場合
2019センター:2点 2018試行調査:45点
(2)数列と統計を選択した場合
2019センター:4点 2018試行調査:48点
(3)ベクトルと統計を選択した場合
2019センター:4点 2018試行調査:52点
さて、これらのグラフの比較から、センター試験よりも共通テスト(あくまでも試行調査ですが)の方が多岐選択式問題が増えたことがわかりました。もう一度確認しておきましょう。
【多岐選択式問題の配点の変化】
▼数学I・数学A
(1)確率と整数を選択した場合
2019センター:25点 2018試行調査:46点
(2)整数と図形を選択した場合
2019センター:25点 2018試行調査:62点
(3)確率と図形を選択した場合
2019センター:25点 2018試行調査:62点
▼「数学II・数学B」
(1)数列とベクトルを選択した場合
2019センター:2点 2018試行調査:45点
(2)数列と統計を選択した場合
2019センター:4点 2018試行調査:48点
(3)ベクトルと統計を選択した場合
2019センター:4点 2018試行調査:52点
さて、これらのグラフの比較から、センター試験よりも共通テスト(あくまでも試行調査ですが)の方が多岐選択式問題が増えたことがわかりました。もう一度確認しておきましょう。
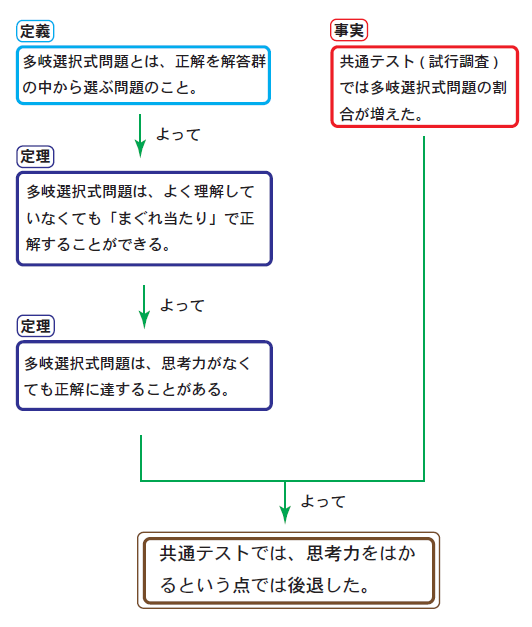 多岐選択式問題とは、正解を解答群の中から選ぶ問題のことです。そしてそれは、よく理解していなくても「まぐれ当たり」で正解することができるため、思考力がなくても正解に達することがあるものです。
しかし、共通テスト(試行調査)では多岐選択式問題の割合が増えています。つまり、共通テストでは、思考力をはかるという点では後退したわけです。
多岐選択式問題が増えた理由として、知識があるかどうかを直接問う問題が増えたからです。従来は計算も必要な問題を出題していて、その問題を解けることで、知識があるかどうか、計算が確実にできるかどうかのように、一題で複数の力を試すしていました。
また、「数学I・数学A」の問題では第1問に2次関数のグラフをコンピュータグラフ表示ソフトの画面があります(2つの試行調査の問題にあります)が、これをわざわざこの設定にする必要はありません。単刀直入に問う方が数学の力があるかどうかを確かめられます。
出題者は何かにとりつかれたような感じで作問しているのが見えます。大変ご苦労なことですが、やはり、共通テストは多くのものを盛り込もうとせずに、シンプルに基礎力をみることに徹した方がよいのではないでしょうか。今のままでは、目的通りのものには程遠い不良品です。日常生活において数学がいかに役に立っているかについては、高校の授業の中で行い、記述式で問いたかったことは、国公立大学の個別試験の中で専門家の目で判定してもらうのがよい形でしょう。
★ここまでのまとめ★
●ここ20年以上前から、数学教育では「数学のよさ」(数学の有用性)をアピールする内容が増えた。
●その結果、数学が実生活の中で役に立つことを教科の中に取り入れられるようになった。
●共通テストにも実生活と関係のある内容を取り入れようとした。その結果、余分な文章を含む長文の問題が現れるようになった。
●一方、答を選択する問題も増えた。これは、思考力がなくても解ける問題でセンター試験と比べると後退した。
●文科省の理想は評価してもよいが、それが実体として現れず、結果として試験としては不良品と見なされることもある。
<文/清史弘>
多岐選択式問題とは、正解を解答群の中から選ぶ問題のことです。そしてそれは、よく理解していなくても「まぐれ当たり」で正解することができるため、思考力がなくても正解に達することがあるものです。
しかし、共通テスト(試行調査)では多岐選択式問題の割合が増えています。つまり、共通テストでは、思考力をはかるという点では後退したわけです。
多岐選択式問題が増えた理由として、知識があるかどうかを直接問う問題が増えたからです。従来は計算も必要な問題を出題していて、その問題を解けることで、知識があるかどうか、計算が確実にできるかどうかのように、一題で複数の力を試すしていました。
また、「数学I・数学A」の問題では第1問に2次関数のグラフをコンピュータグラフ表示ソフトの画面があります(2つの試行調査の問題にあります)が、これをわざわざこの設定にする必要はありません。単刀直入に問う方が数学の力があるかどうかを確かめられます。
出題者は何かにとりつかれたような感じで作問しているのが見えます。大変ご苦労なことですが、やはり、共通テストは多くのものを盛り込もうとせずに、シンプルに基礎力をみることに徹した方がよいのではないでしょうか。今のままでは、目的通りのものには程遠い不良品です。日常生活において数学がいかに役に立っているかについては、高校の授業の中で行い、記述式で問いたかったことは、国公立大学の個別試験の中で専門家の目で判定してもらうのがよい形でしょう。
★ここまでのまとめ★
●ここ20年以上前から、数学教育では「数学のよさ」(数学の有用性)をアピールする内容が増えた。
●その結果、数学が実生活の中で役に立つことを教科の中に取り入れられるようになった。
●共通テストにも実生活と関係のある内容を取り入れようとした。その結果、余分な文章を含む長文の問題が現れるようになった。
●一方、答を選択する問題も増えた。これは、思考力がなくても解ける問題でセンター試験と比べると後退した。
●文科省の理想は評価してもよいが、それが実体として現れず、結果として試験としては不良品と見なされることもある。
<文/清史弘>
前回の記事
ハッシュタグ


