
YouTubeには無数の教育系動画がある。
大学に進学したい、しかし、何らかの理由で塾や予備校に通うことはできない高校生にとって、インターネット上で無料で見ることのできる教育系動画は頼りたくなるツールの一つです。しかし、つい先日も、あるお笑い芸人の方が日本史の動画で看過できないような誤りを伝えていたことが非難されていたように、数学の無料動画にもそのようなものはあります。
現在、教育系無料動画は乱立状態にあり、その多くは善意によるものと思われますが、無責任にケアレスミスではすまされない誤りを流す人もいますので、今回はその見分け方の一つを説明します。
なお、誤解のないように申し上げますと、教育系無料動画を多くの人が個人のアイディアであげること自体はよいことと考えます。多少の余計な話を含んだり、話し方がきつい、字が読みにくいというものは今は許容の範囲内ということにします。以下で触れるのは、内容に決定的な誤りがあり、それを流している本人も理解していないであろう動画-不勉強動画-の見分け方についての説明です。
では、どのようにすれば、不勉強系動画とそうでないかの区別ができるのでしょうか。それの区別がしやすいのは、相加平均と相乗平均の関係を用いて関数の最小値(あるいは最大値)の説明をしている動画を確かめることです。「相加・相乗平均、最小値(最大値)」などと動画検索をすると対象候補があがります。
(※編集部中:以下の数式が見づらい場合は、画像の表示される本サイトの記事を参照してください。)
2変数の相加平均と相乗平均の関係(相加・相乗平均の不等式)とは、正の数x、yについて、
(x+y)/2≧√xy
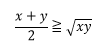
が成り立つことですが、これを利用して関数の最小値を求める場合は、大抵の場合は次の例題を使います。
(1)「x>0のときx+1/xの最小値を求めよ」
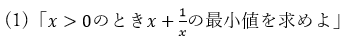
あるいは、
(2)「x>0のときx+4/xの最小値を求めよ。」
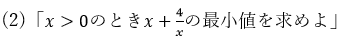
ここでは(1)を例に説明しましょう。(1)の問題を解説するときには、「xと1/xは、かけるとxが消える」(足している2数の積が定数である)ことを強調します。それが、相加平均と相乗平均の関係を用いる「目印」であるというのです。そして、正しく説明する人は次のように説明をします。
【A】相加・相乗平均の不等式より、x+1/x≧2√(x∙1/x)=2、すなわち、x+1/x≧2である。
【B】x=1のとき等号が成り立つ。(「x=1 のとき x+1/x=2となる」の意味)
【C】したがって、x+1/xの最小値は2である。

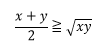 が成り立つことですが、これを利用して関数の最小値を求める場合は、大抵の場合は次の例題を使います。
(1)「x>0のときx+1/xの最小値を求めよ」
が成り立つことですが、これを利用して関数の最小値を求める場合は、大抵の場合は次の例題を使います。
(1)「x>0のときx+1/xの最小値を求めよ」

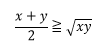 が成り立つことですが、これを利用して関数の最小値を求める場合は、大抵の場合は次の例題を使います。
(1)「x>0のときx+1/xの最小値を求めよ」
が成り立つことですが、これを利用して関数の最小値を求める場合は、大抵の場合は次の例題を使います。
(1)「x>0のときx+1/xの最小値を求めよ」
